Kyle Kingsbury’s Jepsen recently did an analysis of PostgreSQL 12.3 and found that under certain conditions it violated guarantees it makes about transactions, including violations of the serializability transaction isolation level.

I thought it would be fun to use one of his counterexamples to illustrate what serializable means.

Here’s one of the counterexamples that Jepsen’s tool, Elle, found:

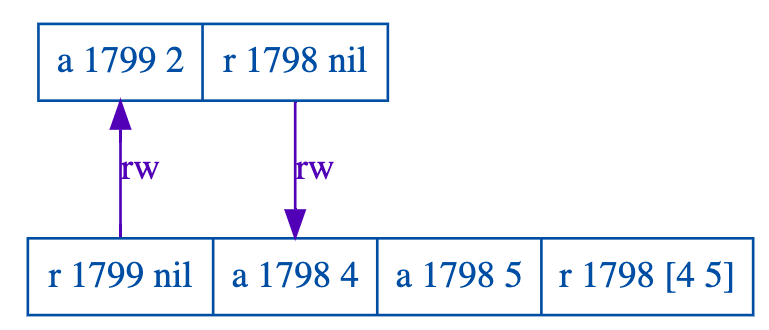
In this counterexample, there are two list objects, here named 1799 and 1798, which I’m going to call x and y. The examples use two list operations, append (denoted "a") and read (denoted "r").

Here’s my redrawing of the example. I’ve drawn all operations against x in blue and against y in red. Note that I’m using empty list ([]) instead of nil.

There are two transactions, which I’ve denoted T1 and T2, and each one involves operations on two list objects, denoted x and y. The lists are initially empty.

For transactions that use the serializability isolation model, all of the operations in all of the transactions have to be consistent with some sequential ordering of the transactions. In this particular example, that means that all of the operations have to make sense assuming either:

• all of the operations in T1 happened before all of the operations in T2
• all of the operations in T2 happened before all of the operations in T1

Assume order: T1, T2

If we assume T1 happened before T2, then the operations for x are:

      x = [] 
T1:   x.append(2)
T2:   x.read() → []

This history violates the contract of a list: we’ve appended an element to a list but then read an empty list. It’s as if the append didn’t happen!

Assume order: T2, T1

If we assume T2 happened before T1, then the operations for y are:

      y = []
T2:   y.append(4)
      y.append(5)
      y.read() → [4, 5]
T1:   y.read() → []

This history violates the contract of a list as well: we read [4, 5] and then [ ]: it’s as if the values disappeared!

Kingsbury indicates that this pair of transactions are illegal by annotating the operations with arrows that show required orderings. The "rw" arrow means that the read operation that happened in the tail must be ordered before the write operation at the head of the arrow. If the arrows form a cycle, then the example violates serializability: there’s no possible ordering that can satisfy all of the arrows.

Serializability, linearizability, locality

This example is a good illustration of how serializability differs from linearizability. Lineraizability is a consistency model that also requires that operations must be consistent with sequential ordering. However, linearizability is only about individual objects, where transactions refer to collections of objects.

(Linearizability also requires that if operation A happens before operation B in time, then operation A must take effect before operation B, and serializability doesn’t require that, but let’s put that aside for now).

This counterexample above is a linearizable history: we can order the operations such that they are consistent with the contracts of x and y. Here’s an example of a valid history, which is called a linearization:

x = []
y = []
x.read() → []
x.append(2)
y.read() → []
y.append(4)
y.append(5)
y.read() → [4, 5]

Note how the operations between the two transactions are interleaved. This is forbidden by transactional isolation, but the definition of linearizability does not take into account transactions.

This example demonstrates how it’s possible to have histories that are linearizable but not serializable.

We say that lineariazibility is a local property where serializability is not: by the definition of linearizability, we can identify if a history is linearizable by looking at the histories of the individual objects (x, y). However, we can’t do that for serializability.